Pitágoras y su Teorema [FÁCIL]
El Teorema de Pitágoras es uno de los teoremas con mayor utilidad. Base en las matemáticas, en geometría, trigonometría, algebra y con amplio uso en la vida cotidiana tal como en la construcción, navegación, topografía, entre otros.
El Teorema de Pitágoras permite encontrar la longitud de los lados de un triángulo rectángulo, y aunque muchos triángulos no son rectángulos, todos se pueden dividir en dos triángulos rectángulos, donde puede aplicarse el Teorema de Pitágoras.
CONCEPTOS BÁSICOS “Para entender el teorema de Pitágoras”
Triángulo:
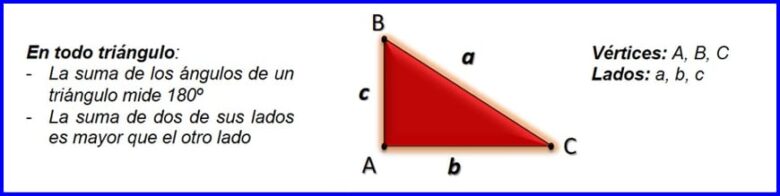
Figura geométrica, en el plano, formada por tres lados que se unen en vértices. Los vértices se escriben en letras mayúsculas y el lado opuesto al vértice con la misma letra minúscula. Ver figura 1. En los triángulos:
- La suma de dos de sus lados es mayor que el otro lado.
- La suma de los ángulos de un triángulo mide 180º.
Clasificación de los triángulos
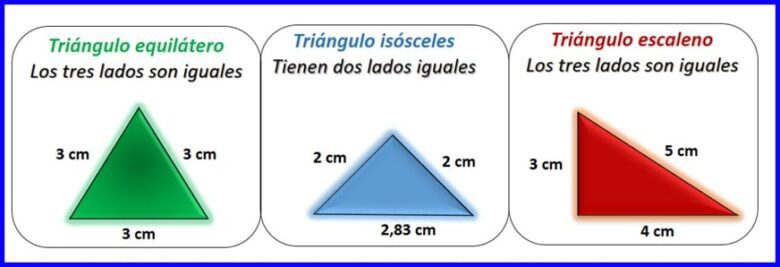
Según la longitud de los lados, un triángulo puede ser equilátero si tiene sus tres lados iguales, isósceles si tiene dos lados iguales o escaleno si ninguno de sus lados son iguales. Ver figura 2.
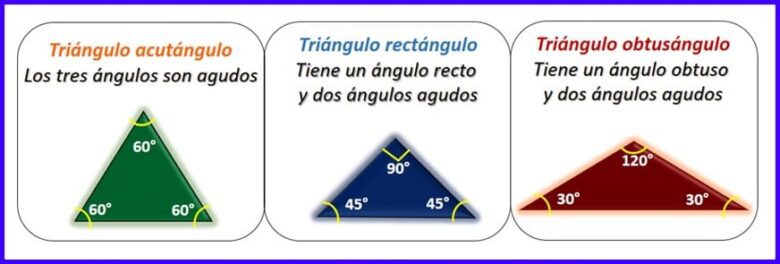
Un ángulo recto es aquel que mide 90°. Si el ángulo es menor de 90° se llama “ángulo agudo”. Si el ángulo es mayor de 90° entonces es llamado “ángulo obtuso”. Según los ángulos, los triángulos se clasifican en:
- Acutángulos: si tienen los 3 ángulos agudos.
- Rectángulos: si tienen un ángulo recto y los otros dos ángulos son agudos.
- Obtusángulos: si tienen un ángulo obtuso y los otros agudos. Ver figura 3.
Triángulo Rectángulo:
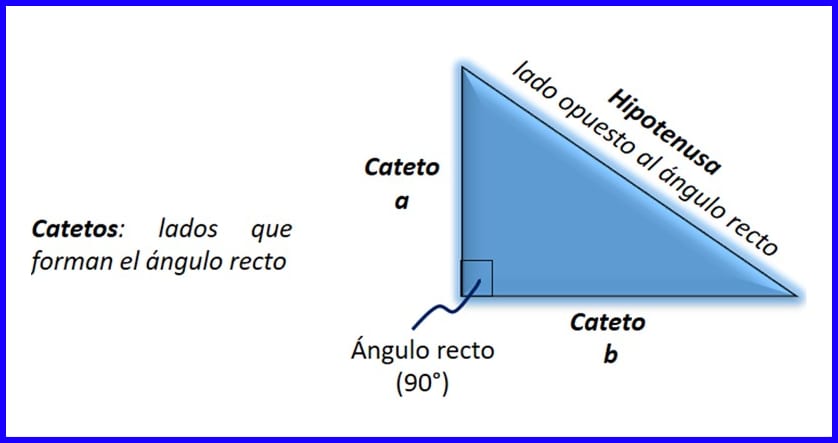
El triángulo rectángulo es aquel con un ángulo recto (de 90°). De los tres lados del triángulo rectángulo, el de mayor longitud es llamado “hipotenusa”, los otros se llaman “catetos” [1]:
- Hipotenusa: lado opuesto al ángulo recto en un triángulo rectángulo. El lado mayor se denomina hipotenusa el que es opuesto al ángulo recto.
- Catetos: es cualquiera de los dos lados menores de un triángulo rectángulo los que conforman el ángulo recto. Ver figura 4.
Teorema de Pitágoras
Enunciado del Teorema de Pitágoras:
El Teorema de Pitágoras establece que, para un triángulo rectángulo, la hipotenusa al cuadrado es igual a la suma de los cuadrados de los dos catetos. [2]. Ver figura 5.

El teorema de Pitágoras también se puede enunciar de la forma siguiente: El cuadrado construido sobre la hipotenusa de un triángulo rectángulo tiene la misma área que la suma de las áreas de los cuadrados construidos sobre los catetos. Ver figura 6.
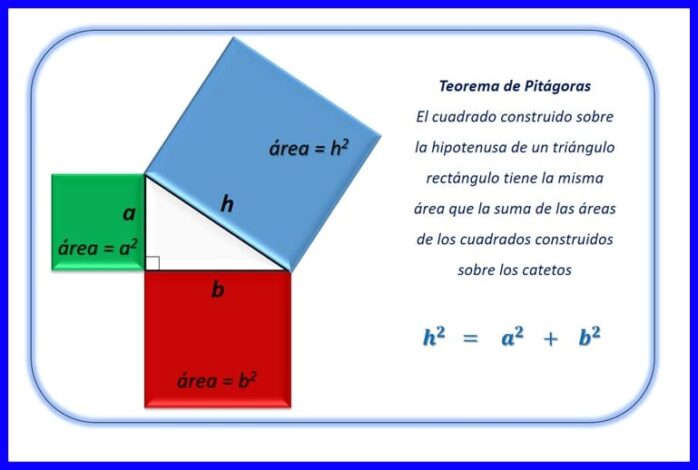
Con el Teorema de Pitágoras se puede determinar la longitud de cualquiera de los lados de un triángulo rectángulo. En la figura 7 se encuentran las fórmulas para hallar la hipotenusa o algunos de los catetos del triángulo.
Usos del teorema de Pitagora
Construcción:
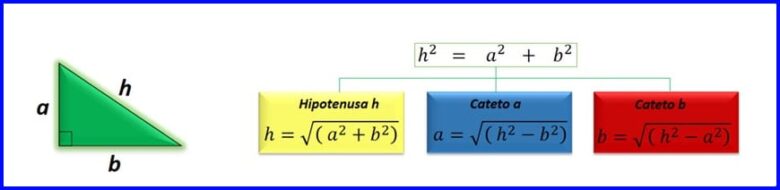
El teorema de Pitágoras es útil en el diseño y construcción de rampas, escaleras, estructuras diagonales, entre otras, por ejemplo, para el cálculo de longitud de un tejado inclinado. En la figura 8 se muestra que para la construcción de las columnas de edificios se emplean caballetes y cuerdas que deben cumplir con el Teorema de Pitágoras.
Topografía:
En la topografía se representa gráficamente, en un plano, la superficie o relieve de un terreno. Por ejemplo, se puede calcular la inclinación de terrenos haciendo uso de una vara de medición, de altura conocida y un telescopio. Entre la línea de visión del telescopio y la vara se forma un ángulo recto, y conocida la altura de la vara se utiliza el teorema de Pitágoras para determinar la pendiente del terreno. Ver figura 8.
Triangulación:
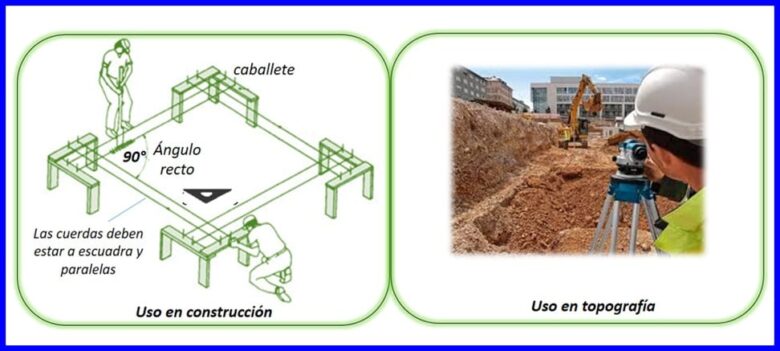
Es un método usado para determinar la ubicación de un objeto, conocidos dos puntos de referencia. La triangulación se utiliza en el rastreo de teléfonos celulares, en sistemas de navegación, en la detección de una nave en el espacio, entre otras. Ver figura 9.
¿Quién fue Pitágoras?
Pitágoras nació en Grecia el año 570 a.c, falleció en el año 490 a.c. Fue filósofo y matemático. Tenía como filosofía que cada número tenía un significado divino, y la combinación de los números revelaba otros significados. A pesar de que no realizó publicaciones de ningún escrito durante toda su vida, es conocido por introducir el teorema que lleva su nombre, útil para el estudio de triángulos. Se considera el primer matemático puro, que desarrolló estudios matemáticos en geometría y astronomía. [2]. Ver figura 10.

Ejercicios
Para utilizar el Teorema de Pitágoras lo primero a hacer es identificar donde se forma el triángulo rectángulo, cuál de los lados es la hipotenusa y los catetos.
Ejercicio 1. Determine el valor de la hipotenusa para el triángulo rectángulo de la figura
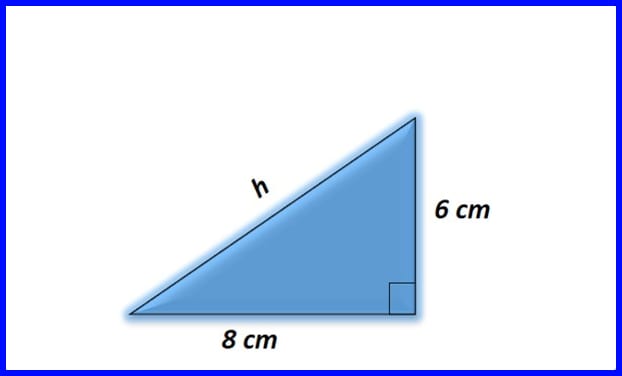
Solución:
En la figura 12 se muestra el cálculo de la hipotenusa del triángulo.

Ejercicio 2. Se requiere sostener un poste mediante un conjunto de tres cables, tal como se muestra en la figura 13. ¿Cuántos metros de cable se deben comprar?
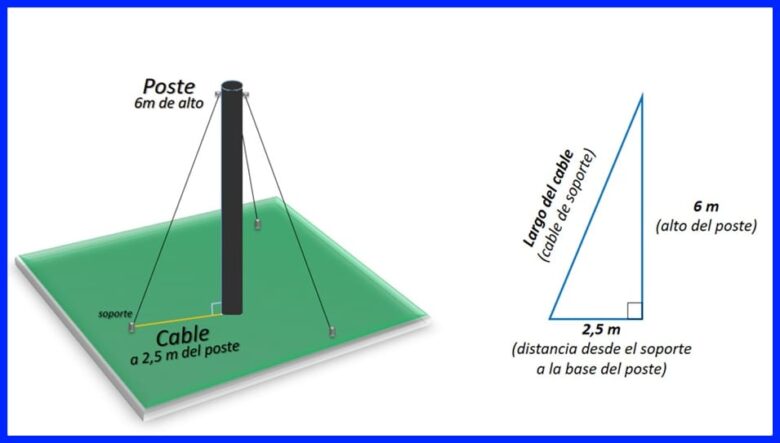
Solución
Si se considera el cable como la hipotenusa de un triángulo rectángulo que se forma entre el cable, el poste y el suelo, se determina la longitud de uno de los cables usando el teorema de Pitágoras. Ya que son tres cables, la longitud obtenida se multiplica por 3 para obtener la longitud total necesaria. Ver figura 14.

Ejercicio 3. Para transportar unas cajas, desde un segundo piso a planta baja, se desea adquirir una banda transportadora inclinada como la mostrada en la figura 15. ¿Qué longitud debe tener la cinta transportadora?
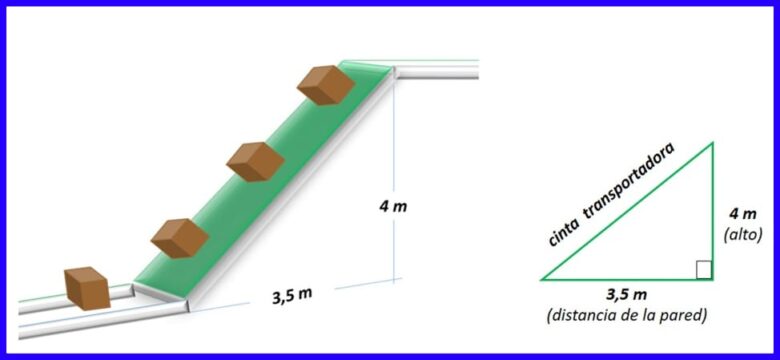
Solución:
Considerando la banda transportadora como la hipotenusa del triángulo rectángulo que se forma entre la banda, el suelo y la pared, en la figura 16 se calcula la longitud de la cinta transportadora.

Ejercicio 4. Un carpintero diseña un mueble donde deben ir unos libros, y un televisor de 26”. ¿qué ancho y alto debe tener la división donde irá el televisor? Ver figura 17.

Solución:
La medida que se utiliza en dispositivos electrónicos tales como teléfonos, tablets, televisores, entre otros en la de la diagonal de la pantalla. Para un televisor de 26”, la diagonal de la pantalla mide 66,04 cm. Considerando el triángulo rectángulo que se forma con la diagonal de la pantalla, y los lados del televisor, se puede aplicar el teorema de Pitágoras para determinar el ancho del televisor. Ver figura 18.

Conclusiones sobre el Teorema de Pitágoras
El Teorema de Pitágoras permite encontrar la longitud de los lados de un triángulo rectángulo, y aun para cualquier otro triángulo, ya que éstos pueden dividirse en triángulos rectángulos.
El Teorema de Pitágoras indica que el cuadrado de la hipotenusa de un triángulo rectángulo es igual a la suma del cuadrado de los catetos, siendo de gran utilidad en el estudio de la geometría, trigonometría, y matemática en general, con amplio uso en la construcción, navegación, topografía, entre otras tantas aplicaciones.
Los invitamos a ver el articulo Leyes de Newton “fácil de entender”
