Gracias a los estudios de los científicos se ha logrado comprender los fenómenos de la naturaleza, y realizar avances tecnológicos a través de los años. Newton, basado en los estudios de Galileo sobre las leyes que rigen el movimiento de proyectiles en la Tierra, y los estudios de Kepler sobre las leyes del movimiento de los planetas en el sistema solar, concluye que la fuerza necesaria para mantener a un planeta en una órbita depende de las masas y de la distancia de separación. La ley de gravitación universal, publicada en 1687 por Isaac Newton, permite determinar la fuerza con la que se atraen dos objetos con masa, siendo de gran utilidad en el estudio de las órbitas de los cometas, el descubrimiento de otros planetas, las mareas, el movimiento de los satélites, entre otros fenómenos.
Conceptos Básicos para entender “Ley de Gravitación Universal”
Los invitamos a ver el artículo Leyes-de-Newton-fácil-de-entender
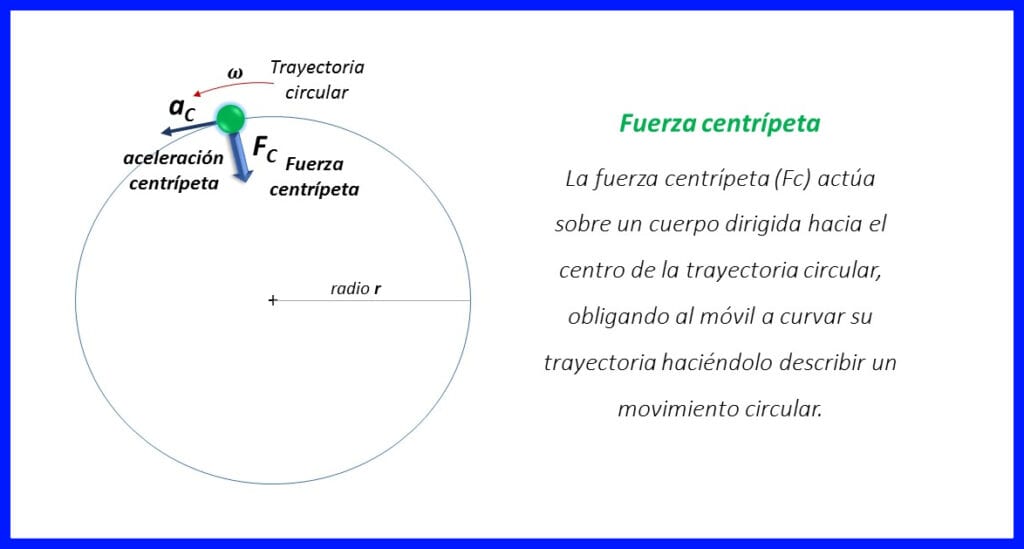
Fuerza centrípeta:
Fuerza que obliga al móvil a curvar su trayectoria haciéndolo describir un movimiento circular. La fuerza centrípeta actúa sobre un cuerpo dirigida hacia el centro de la trayectoria circular. El cuerpo experimenta una aceleración centrípeta ya que la velocidad, de módulo constante, cambia de dirección al moverse. Ver figura 1.
La fuerza centrípeta se puede calcular usando la segunda ley de Newton [1], donde la aceleración centrípeta se puede expresar en función a la velocidad angular, a la velocidad lineal, o en función al período del cuerpo en movimiento circular. Ver figura 2.
[adinserter name=”Bloque 1″]Leyes de Kepler
El astrónomo Johannes Kepler explico el movimiento de los planetas del sistema solar, mediante tres leyes: ley de las órbitas, de las áreas y de los periodos. [2].
Primera ley de Kepler, o ley de las órbitas:
todos los planetas, del sistema solar, giran alrededor del sol describiendo una órbita en forma de elipse. El sol se encuentra en uno de los dos focos de la elipse. Ver figura 3.
La segunda ley de Kepler, o ley de las áreas:
El radio que une a un planeta con el sol describe áreas iguales en tiempos iguales. La línea (imaginaria) que va del sol a un planeta, barre áreas iguales en tiempos iguales; es decir, que la velocidad a la que cambia el área, es constante. Ver figura 4.
Tercera ley de Kepler, o ley de los periodos:
Para todos los planetas, la relación entre el cubo del radio de la órbita y el cuadrado de su periodo es constante. El eje mayor de la elipse elevada al cubo y dividida entre el período (lapso en dar una vuelta entera), es una misma constante para los diferentes planetas. La energía cinética de un planeta decrece como el inverso de su distancia al sol. Ver figura 5.
Ley de Gravitación Universal
La ley de gravitación universal, publicada en 1687 por Isaac Newton, permite determinar la fuerza con la que se atraen dos objetos con masa. Newton concluyo que:
- Los cuerpos se atraen por el solo hecho de poseer masa.
- La fuerza de atracción entre los cuerpos solo es notoria cuando al menos uno de los cuerpos que interactúan es enormemente grande, como un planeta.
- Hay una interacción a distancia, por tanto, no es necesario que los cuerpos estén en contacto para que la fuerza de atracción actúe.
- La interacción gravitatoria entre dos cuerpos siempre se manifiesta como un par de fuerzas iguales en dirección y módulo, pero en sentido contrario.
Enunciado de la Ley de Gravitación Universal
La fuerza de atracción entre dos masas es directamente proporcional al producto de las masas e inversamente proporcional al cuadrado de la distancia que las separa. La fuerza de atracción tiene una dirección que coincide con la recta que los une.[3]. Ver figura 6.
La constante de proporcionalidad G entre las magnitudes se conoce con el nombre de constante de gravitación universal. En el sistema internacional equivale a:
Ejercicio 1. Determinar la fuerza con la que se atraen, en el vacío, los cuerpos de la figura 7.
Solución
En la figura 8 se tienen dos cuerpos con masas m1=1000 kg y m2=80 kg, separados por una distancia de 2 metros. Aplicando la ley de gravitación universal se puede determinar la fuerza de atracción entre éstos, tal como se muestra en la figura 8.
Deducción de la Ley de Gravitación Universal
Partiendo de la tercera ley de Kepler que relaciona el radio con el periodo de un planeta en órbita, la aceleración centrípeta que experimenta un planeta, es inversamente proporcional al cuadrado del radio de su órbita. Para hallar la fuerza centrípeta que actúa sobre el planeta se utiliza la segunda ley de Newton [], considerando la aceleración centrípeta que experimenta, expresada en función al período. Ver figura 9.
El valor de la constante de gravitación universal fue determinada por Henry Cavendish muchos años después de establecida la ley de gravitación por Newton. La constante G se considera “universal” ya que su valor es el mismo en cualquier parte del universo conocido, y es independiente del medio en el que se encuentren los objetos.
Ejercicio 2. Determinar la masa del planeta Tierra, sabiendo que el radio es de 6380 km
Solución
Los cuerpos ubicados en la superficie de la tierra son atraídos hacia su centro, esta fuerza es la conocida como el peso de un cuerpo (fuerza con que la Tierra lo atrae). Por otra parte, se puede aplicar la segunda ley de Newton expresando el peso del cuerpo en función a la gravedad, así se puede obtener la masa de la Tierra, conocida su radio. Ver figura 11.
Aplicación de la ley de gravitación universal
La ley de gravitación universal es útil para explicar la órbita de los cometas, el descubrimiento de otros planetas, las mareas, el movimiento de los satélites, entre otros fenómenos.
Las leyes de Newton se cumplen con exactitud, cuando se observa que algún astro no la cumple es porque algún otro astro no visible perturba el movimiento, así se han descubierto la existencia de planetas a partir de la perturbación que producen en las órbitas de planetas conocidos.
Satélites:
Un satélite es un objeto que orbita alrededor de otro objeto de mayor tamaño y mayor campo gravitatorio, por ejemplo, se tiene la luna, el satélite natural del planeta Tierra. Un satélite experimenta una aceleración centrípeta debido a que se encuentra sometido a una fuerza de atracción en el campo gravitatorio.
Ejercicio 3. Determinar la velocidad de un satélite que órbita alrededor de la tierra a 6870 km del centro de la Tierra. Ver figura 12
Solución
Los satélites artificiales se mantienen en órbita alrededor de la Tierra debido a la fuerza de atracción que ejerce la Tierra sobre el mismo. Usando la ley de gravitación universal y la segunda ley de Newton se puede determinar la velocidad del satélite. Ver figura 13.
CONCLUSIONES
Toda partícula material atrae a cualquier otra partícula material con una fuerza directamente proporcional al producto de las masas de ambas e inversamente proporcional al cuadrado de la distancia que las separa.
La interacción gravitatoria entre dos cuerpos siempre se manifiesta como un par de fuerzas iguales en dirección y módulo, pero en sentido contrario.
La ley de gravitación universal de Newton permite determinar la fuerza con la que se atraen dos objetos con masa, sabiendo que la fuerza de atracción entre dos masas es directamente proporcional al producto de las masas e inversamente proporcional al cuadrado de la distancia que las separa.