فيثاغورس ونظريته [سهل]
نظرية فيثاغورس إنها واحدة من أكثر النظريات فائدة. قاعدة في الرياضيات والهندسة وعلم المثلثات والجبر وتستخدم على نطاق واسع في الحياة اليومية مثل البناء والملاحة والتضاريس وغيرها.
نظرية فيثاغورس يسمح لك بإيجاد طول أضلاع المثلث القائم ، وعلى الرغم من أن العديد من المثلثات غير صحيحة ، إلا أنه يمكن تقسيمها جميعًا إلى مثلثين قائم الزاوية ، حيث يمكن تطبيق نظرية فيثاغورس.
المفاهيم الأساسية "لفهم نظرية فيثاغورس"
مثلث:
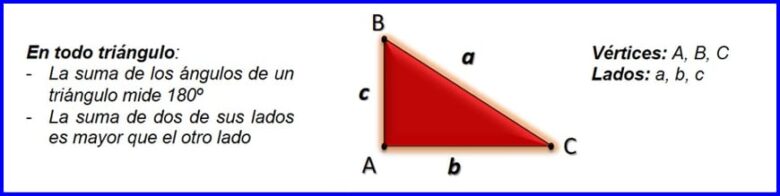
شكل هندسي ، في المستوى ، يتكون من ثلاثة جوانب تلتقي عند الرؤوس. تتم كتابة الرؤوس بأحرف كبيرة والجانب المقابل للرأس بنفس الحرف الصغير. انظر الشكل 1. في المثلثات:
- مجموع ضلعين له أكبر من الضلع الآخر.
- مجموع زوايا المثلث 180º.
تصنيف المثلثات
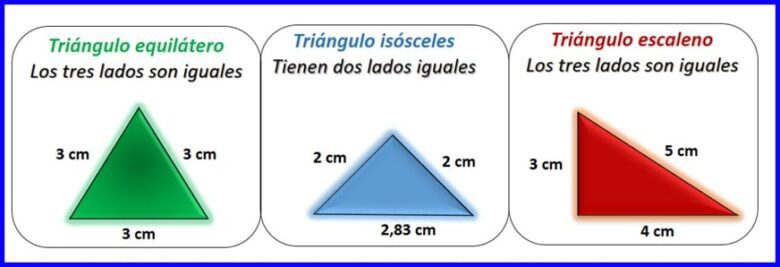
اعتمادًا على طول الأضلاع ، يمكن أن يكون المثلث متساوي الأضلاع إذا كان له ثلاثة جوانب متساوية ، أو متساوي الساقين إذا كان له جانبان متساويان ، أو مقياس إذا لم يكن أي من ضلعه متساويًا. انظر الشكل 2.
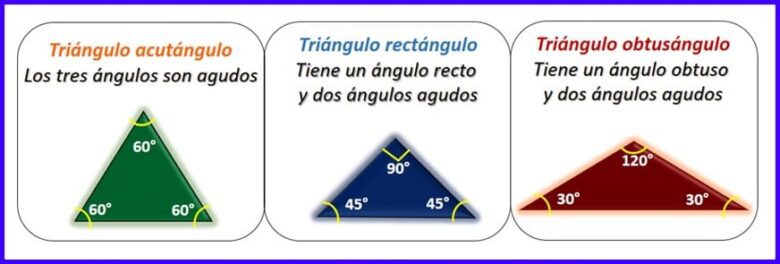
الزاوية القائمة هي التي قياسها 90 درجة. إذا كانت الزاوية أقل من 90 درجة تسمى "الزاوية الحادة". إذا كانت الزاوية أكبر من 90 درجة فإنها تسمى "الزاوية المنفرجة". حسب الزوايا تصنف المثلثات إلى:
- زوايا حادة: إذا كان لديهم 3 زوايا حادة.
- المستطيلات: إذا كان لديهم زاوية قائمة والزاويتان الأخريان حادتان.
- زوايا حادة: إذا كان لديهم زاوية منفرجة والأخرى حادة. انظر الشكل 3.
مثلث قائم:
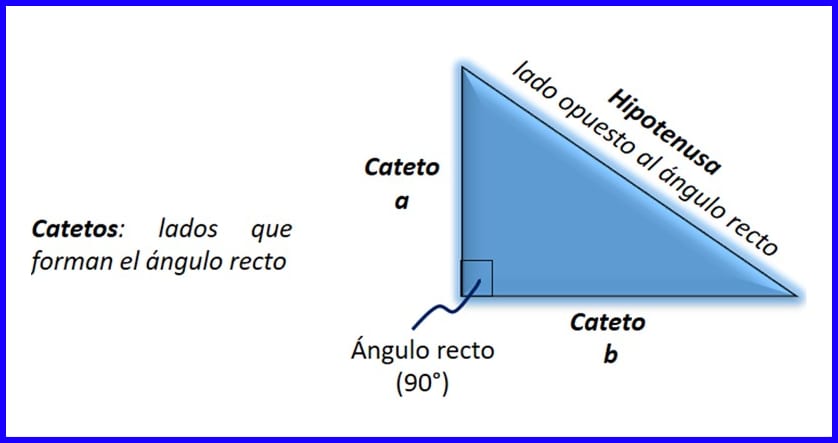
المثلث القائم الزاوية هو واحد بزاوية قائمة (90 درجة). من بين الأضلاع الثلاثة للمثلث الأيمن ، يُطلق على أطولها "الوتر" ، بينما يُطلق على الجوانب الأخرى اسم "الأرجل" [1]:
- الوتر: الضلع المقابل للزاوية القائمة في مثلث قائم الزاوية. يسمى الضلع الأطول الوتر وهو المقابل للزاوية القائمة.
- الأرجل: إنه أحد ضلعي المثلث القائم الزاوية الأصغر حجمًا الذي يشكل الزاوية القائمة. انظر الشكل 4.
فيثاغورس نظرية
بيان نظرية فيثاغورس:
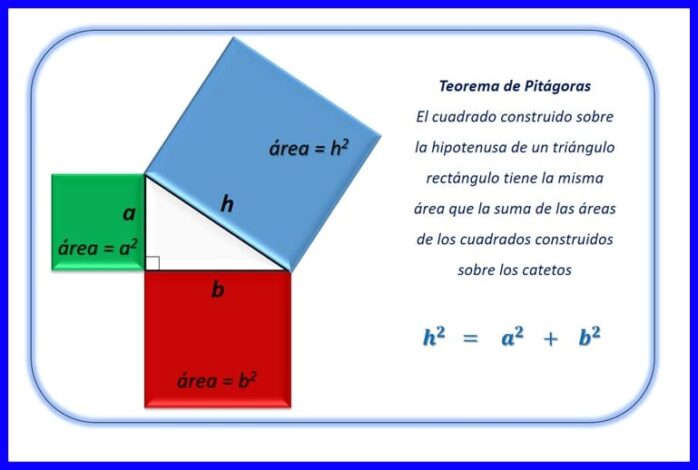
نظرية فيثاغورس ينص على أن تربيع وتر المثلث القائم الزاوية يساوي مجموع مربعي الساقين. [اثنين]. انظر الشكل 2.

نظرية فيثاغورس يمكن أيضًا ذكرها على النحو التالي: المربع المبني على وتر المثلث الأيمن له نفس مساحة مجموع مساحات المربعات المبنية على الأرجل. انظر الشكل 6.
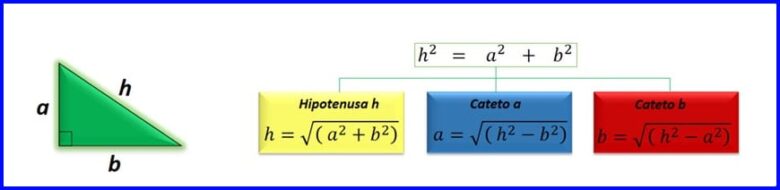
مع فيثاغورس نظرية يمكنك تحديد طول جانبي المثلث القائم. في الشكل 7 توجد صيغ لإيجاد الوتر أو بعض أرجل المثلث.
استخدامات نظرية فيثاغورا
البناء:
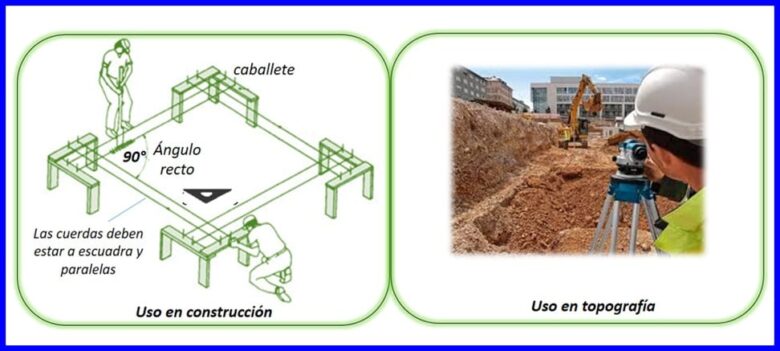
نظرية فيثاغورس إنه مفيد في تصميم وبناء المنحدرات والسلالم والهياكل القطرية ، من بين أمور أخرى ، على سبيل المثال ، لحساب طول السقف المنحدر. يوضح الشكل 8 أنه لبناء أعمدة البناء ، يتم استخدام الحوامل والحبال التي يجب أن تتوافق مع نظرية فيثاغورس.
التضاريس:
في التضاريس ، يتم تمثيل سطح أو تضاريس التضاريس بيانياً على مستوى. على سبيل المثال ، يمكن حساب ميل التضاريس باستخدام قضيب قياس بارتفاع معروف وتلسكوب. تتشكل الزاوية اليمنى بين خط رؤية التلسكوب والقضيب ، وبمجرد معرفة ارتفاع القضيب ، تُستخدم نظرية فيثاغورس لتحديد منحدر التضاريس. انظر الشكل 8.
التثليث:
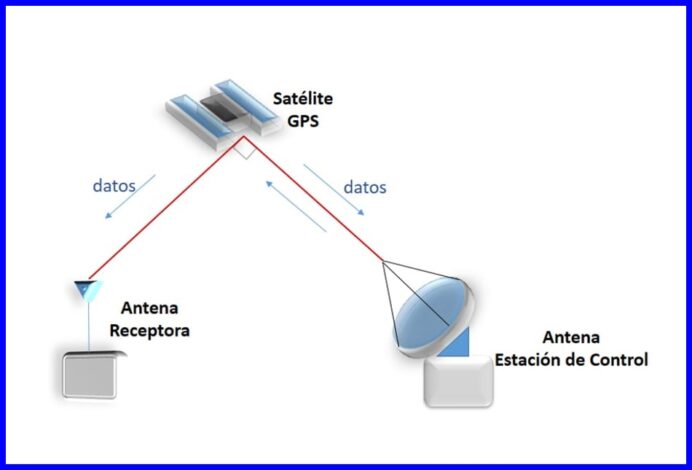
إنها طريقة تستخدم لتحديد موقع كائن ما ، معروف بنقطتين مرجعيتين. يستخدم التثليث في تتبع الهواتف المحمولة ، في أنظمة الملاحة ، في اكتشاف سفينة في الفضاء ، من بين أمور أخرى. انظر الشكل 9.
من كان فيثاغورس؟
ولد فيثاغورس في اليونان عام 570 قبل الميلاد ، وتوفي عام 490 قبل الميلاد ، وكان فيلسوفًا وعالمًا في الرياضيات. كانت فلسفته أن كل رقم له معنى إلهي ، وأن الجمع بين الأرقام يكشف عن معاني أخرى. على الرغم من أنه لم ينشر أي كتابات طوال حياته ، إلا أنه معروف بتقديم النظرية التي تحمل اسمه ، والمفيدة لدراسة المثلثات. يعتبر أول عالم رياضيات نقي طور دراسات رياضية في علم الهندسة وعلم الفلك. [اثنين]. انظر الشكل 2.

حفر
لاستخدام نظرية فيثاغورس ، فإن أول شيء يجب فعله هو تحديد مكان تشكل المثلث القائم ، أي من الأضلاع هو الوتر والساقين.
تمرين 1. حدد قيمة الوتر للمثلث القائم الزاوية في الشكل
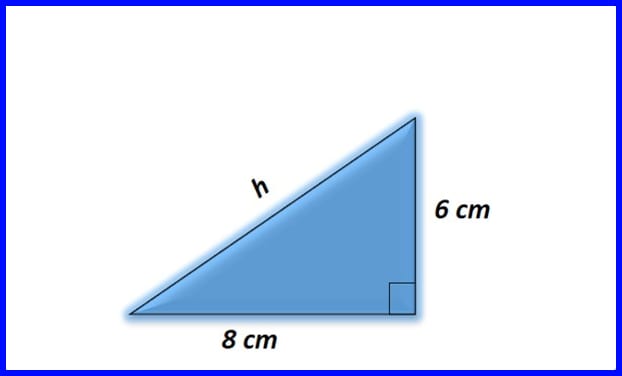
حل:
يوضح الشكل 12 حساب وتر المثلث.

تمرين 2. مطلوب عمود ليتم دعمه بمجموعة من ثلاثة كبلات ، كما هو موضح في الشكل 13. ما هو عدد الأمتار من الكابلات التي يجب شراؤها؟
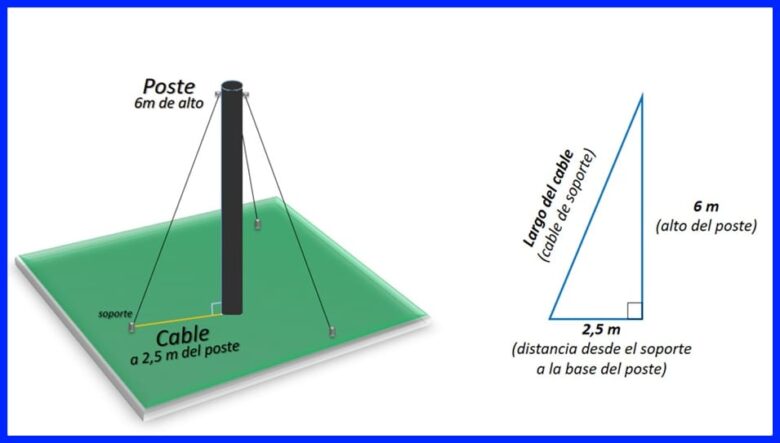
حل
إذا اعتبر الكبل بمثابة وتر المثلث القائم بين الكبل والقطب والأرض ، فسيتم تحديد طول أحد الكبلات باستخدام نظرية فيثاغورس. نظرًا لوجود ثلاثة كبلات ، يتم ضرب الطول الذي تم الحصول عليه في 3 للحصول على الطول الإجمالي المطلوب. انظر الشكل 14.

التمرين 3. لنقل بعض الصناديق ، من الطابق الثاني إلى الطابق الأرضي ، تريد شراء حزام ناقل مائل مثل الحزام الموضح في الشكل 15. ما طول حزام النقل؟
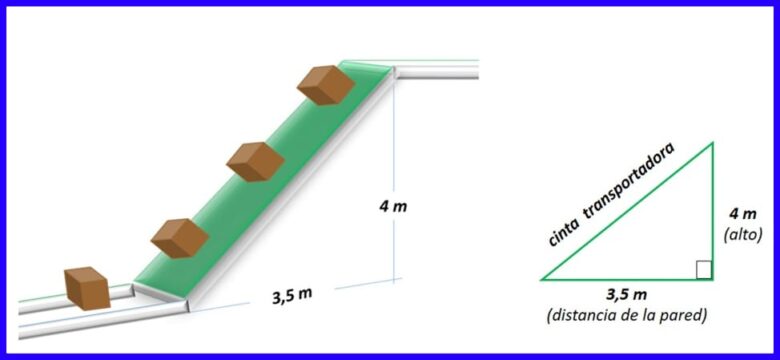
حل:
بالنظر إلى الحزام الناقل على أنه وتر المثلث الأيمن المتكون بين الحزام والأرض والجدار ، في الشكل 16 ، يتم حساب طول الحزام الناقل.

تمرين 4. نجار يصمم قطعة أثاث في مكان توضع فيها الكتب ، وجهاز تلفزيون مقاس 26 بوصة. ما هو العرض والارتفاع الذي يجب أن يكون عليه القسم حيث سيذهب التلفزيون؟ انظر الشكل 17.

حل:
القياس المستخدم في الأجهزة الإلكترونية مثل الهواتف والأجهزة اللوحية والتلفزيونات وغيرها ، في قطر الشاشة. بالنسبة لتلفزيون مقاس 26 بوصة ، يبلغ قطر الشاشة 66,04 سم. بالنظر إلى المثلث الأيمن المتكون من قطر الشاشة وجوانب التلفزيون ، يمكن تطبيق نظرية فيثاغورس لتحديد عرض التلفزيون. انظر الشكل 18.

استنتاجات في نظرية فيثاغورس
نظرية فيثاغورس يسمح لك بإيجاد طول أضلاع المثلث القائم ، وحتى لأي مثلث آخر ، حيث يمكن تقسيمها إلى مثلثات قائمة.
نظرية فيثاغورس يشير إلى أن مربع وتر المثلث الأيمن يساوي مجموع مربع الساقين ، وهو مفيد جدًا في دراسة الهندسة وعلم المثلثات والرياضيات بشكل عام ، مع الاستخدام الواسع في البناء والملاحة والتضاريس ، من بين العديد من التطبيقات الأخرى.
نحن ندعوك لرؤية المقال قوانين نيوتن "سهلة الفهم"
